Precision in DST
a learning experience
|
Mou's Dimensional Shuffle Transform patents define "Precision" as a ratio of
set sizes or cardinalities. We are given a finite and discrete "space" of length $2^W$ in each of K dimensions, and the transform and inverse transform dst(p), idst(k) relating points in the K-d space with keys in the corresponding key space. In a rectangular search query we are given points $p_s$ and $p_t$ with each coordinate of $p_s$ less than or equal to the corresponding coordinate of $p_t$. $p_s$ and $p_t$ are corners of the rectangular search region. A regular region $\lt p_s,p_t\gt$ is the set of points
$\{ p = (x,y,..)\ |\ x_s \le x \le x_t, y_s \le y \le y_t\ ... \}$A linear region [s,t] is set of keys $\{ k\ |\ s \le k \le t \}$ The cardinality of the linear region is
$ |\ [s,t]\ | = t-s+1$The cardinality of the regular region is the product of the dimensional spans
$ |\ \lt p_s,p_t\gt\ | = (x_t-x_s+1)\ *\ (y_t-y_s+1)\ *\ ... $The precision is the ratio of their cardinalities:
Precision $(W,K,s,t) = \frac{|\ [s,t]\ |}{| \lt s,t\gt |} $For $W = 2, K = 2, p_s = (1,1), p_t = (2,2)$ we have a 4x4 space with coordinates ranging from 0 to 3 in both x and y dimensions, as laid out in the table below, each cell giving various descriptions of its location. I place point (0,0) in upper right, and count x starting from 0 increasing to the right and y also zero-based increasing downward. Each cell contains the coordinates (x,y), the bit pattern formed by concatenating the bits of x with the bits of y, then <> indicating the dst/idst bidirectional transform, then the key in the form of the bit pattern resulting from the transform, then last the key in the form of a decimal number. The regular region p_s=(1,1) to p_t = (2,2) is outlined with a black border.
Note the linear region or keyspan
The precision of the non-decomposed search region (1,1) to (2,2) is
therefore 4/10 = 0.4.
Now a 2-way geometric decomposition of the <3,12> keyspan would
include the four following linear subregions: <3,3>, <4,7>, <8,11> and
<12,12>, with precisions, respectively, of 1, 1/4, 1/4, and 1.
Mou claims that when a search region is decomposed, the precision
always increases. In this case 0.4 increases for two of the
subregions to 1.0 but decreases in the other two subregions to 0.25.
I infer not that I am right and George is wrong, but that I do not
understand George's definitions either of precision or of
decomposition.
Please correct my understanding.
To self-correct, I read the patent again extra carefully, and the
issue is the definition of decomposition. George does NOT use
geometric decomposition, by merely cutting the regular region by
planes aligned with certain bits at a certain Level. That approach
would retain the large and mostly-empty sub-keyspans, as in the above
example <4,7> and <8,11> --- empty, because most data spread over those
locations are outside the search region.
Instead George neatly defines the constructs LowerFront, UpperBack,
and ChooseDimensions, as as to precisely construct keys associated
with the critical sub-region corners -- which contain the critical
sub-region boundary coordinates -- and combines them into the
canonical search corners for each sub-region, all in key space. I
have finally been able to understand what he is doing after drawing a
picture of these points with their keys and coordinates all on an
arbitrarily-zoomed bit of 2D geometric space. On the drawing also are
placed the points/keys/coordinates of the constructed LowerFront and
UpperBack corners as well, which abut one another on the zero-one
boundaries at the highest-significance cutting planes through the
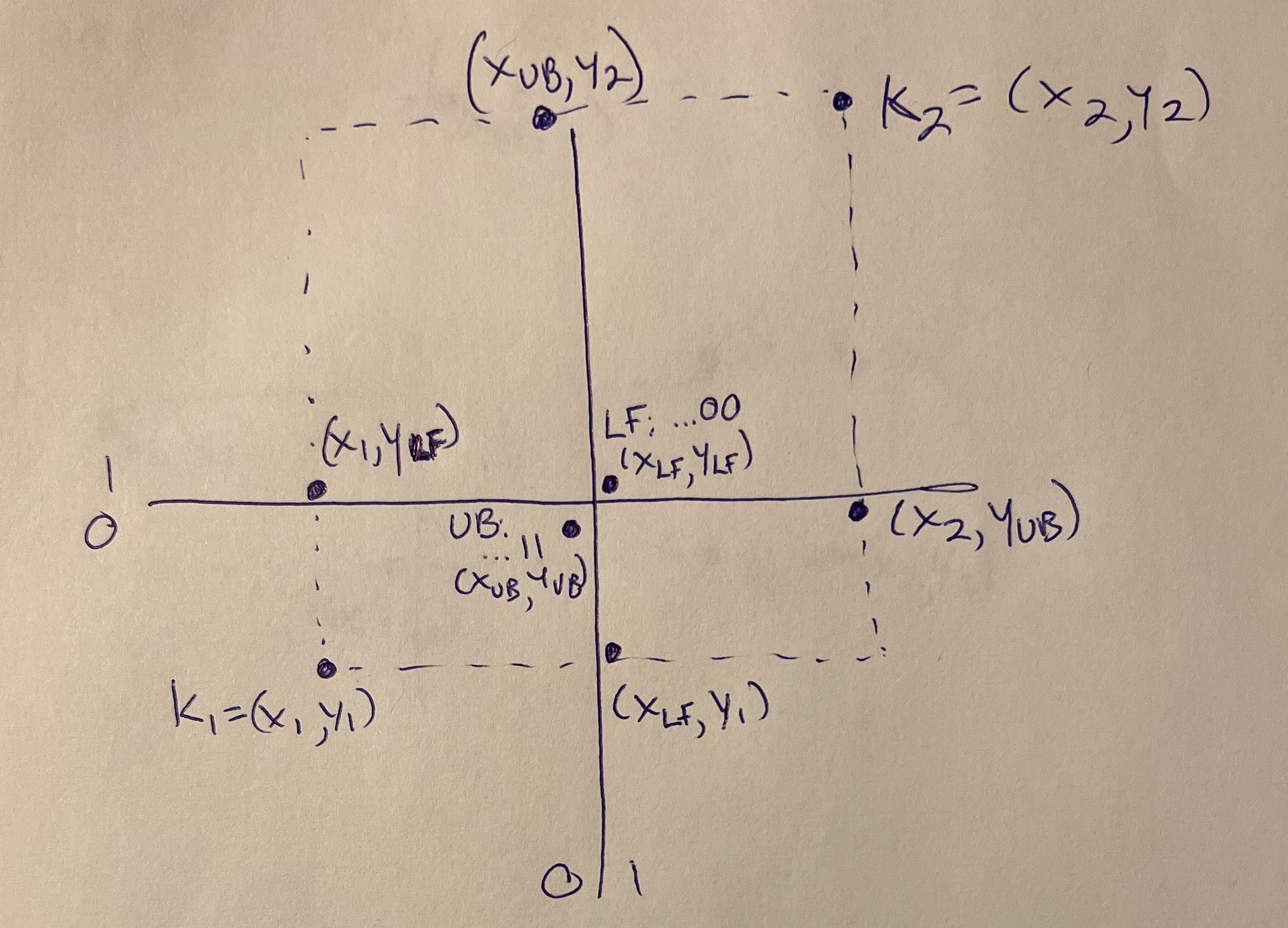
search region. See here a photo of my hand drawing.
This shows two planes cutting the search region into four sub-regions.
The search region is defined by canonical corner points with keys $k_1$ and $k_2$
and coordinates $(x_1,y_1)$ and $(x_2,y_2)$.
UpperBack constructs the UB point's key by adjusting the bits in $k_1$
setting all the lower bits to one, which amounts to moving to the
highest point in its subregion. This is the point defining the
opposite corner for a canonical search of that subregion. LowerFront
constructs the LF point's key by adjusting the bits of $k_2$, setting
its lower bits to zero, which amounts to moving to the lowest point in
its subregion, which is also the point defining the opposite corner
for a canonical search of that subregion. Importantly, UB and LF abut each other
across the dividing plane(s), and contain the highest and lowest, respectively, coordinates
within all the dimensions at that bit level. We can use them to define the coordinates
of all the subregions!
Now the two subregions with a corner that is a corner of the original
search region are obviously: $\lt k_1, k_{UB} \gt \iff \lt (x_1,y_1),
(x_{UB},y_{UB}) \gt $, the first subregion, and $\lt k_{LF},k_2 \gt \iff
\lt (x_{LF},y_{LF}), (x_2,y_2) \gt $, the last subregion.
Two beautiful realizations give us the other subregions, tightly
bounded -- unlike the bounds from a geometric decomposition at the
search keys' Level, which I was assuming as I constructed my above,
supposed counterexample to George's theorem.
First, the other subregions, although they do NOT share any corner with
the original search region, DO share one or another COORDINATE with the
coordinates of the original corners. We can use $x_1$ or $y_1$ or $x_2$ or $y_2$
as ONE of the coordinates of the other subregion corners.
The second beautiful realization is that we can use the different
coordinates of the UpperBack and LowerFront points as the OTHER
coordinate, for each corner of these other subregions. Have a look at
how the upper left subregion, for example, is defined by its corners
$(x_1,y_{LF})$ to $(x_{UB},y_2)$.
These two simple insights are quite obvious when looked at a certain
way, yet still it is not obvious how to combine what bits to make it
work. The insights follow from the rectangular box character of every
search box as a mere tautology, we can construct the canonical corners
of every subregion by combining the various coordinates of $p_1, p_2,
p_{UB}, p_{LF}$ as appropriate, by just reading them off the drawing.
In fact even though this discussion assumes a 2D DST, the same
conceptual approach applies to 3D and higher.
Now to achieve even a higher level of heroic simplification, we would
like to also do the work here of combining the coordinates so chosen,
all within keyspace, by binary operations on keys yielding keys,
without converting back and forth into geometric coordinates. The
requirement would be to be able to extract from a key just the X
dimension's bits, and to combine them from another key's Y-dimension
bits (etc...Z...) so as to directly construct the key of a point that
defines the desired corner of a given subregion. With that function,
$C(k_1,k_2,k_3)$ in the 2023 patent, the operations are done entirely
on the bit patterns of keys without transformation back into geometric
coordinates. Nice!
All right, thank you George. You posed me a challenge, namely, keep
reading it until you understand it, and I feel I have found a bit of
success. Very well.
|